Other Exercises. Question 1. Find the sum of n terms of the series: (i) 4 + 44 + 444 +. (ii) 0.8 + 0.88 + 0.888 +.

1. Selena Publishers Concise Mathematics Class 7 Guide
2. Selina Publishers Concise Mathematics For Class 7 Solutions Pdf

Solution: (i) 4 + 44 + 444 +. = Question 2. Find the sum of infinite terms of each of the following geometric progression: (i) (ii) (iii) (iv) (v) Solution: (i) upto infinity S n = Question 3. The second term of a G.P. Is 9 and sum of its infinite terms is 48.

May 22, 2018 - APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 7 Mathematics. You can download the Selina.

Find its first three terms. Solution: In a G.P. T 2 = 9, sum of infinite terms = 48 Let a be the first term and r be the common ratio, therefore, S ∞ = Question 4. Find three geometric means between and 432. Solution: Let G 1, G 2 and G 3 be three means between and 432, then Question 5.

The package includes a series of exams for each chapter taken by email and a final exam in the same way. Upon successful completion of the final exam, an FAA accredited GenFam certificate is issued for that aircraft. B 777 instructor manual.

Find: (i) two geometric means between 2 and 16 (ii) four geometric means between 3 and 96. (iii) five geometric means between and. Solution: (i) Two G.M. Between 2 and 16 Let G 1, and G 1 be the G.M., then 2, G 1, G 2, 16 Question 6. The sum of three numbers in G.P. Is and their product is 1. Find numbers Solution: Sum of three numbers in G.P = and their product = 1 Question 7.

Find the numbers in G.P. Whose sum is 52 and the sum of whose product in pairs is 624.

Solution: Sum of 3 numbers in G.P. = 52 and their product in pairs = 624 Let numbers be a, ar, ar² Question 8. The sum of three numbers in G.P. Is 21 and the sum of their squares is 189. Find the numbers.

Solution: Sum of three numbers in G.P. = 21 Sum of their squares = 189 Let three numbers be a, ar, ar², then a + ar + ar² = 21 = a( 1 + r + r²) = 21.(i) Hope given are helpful to complete your math homework. If you have any doubts, please comment below. Try to provide online math tutoring for you.

Selena Publishers Concise Mathematics Class 7 Guide

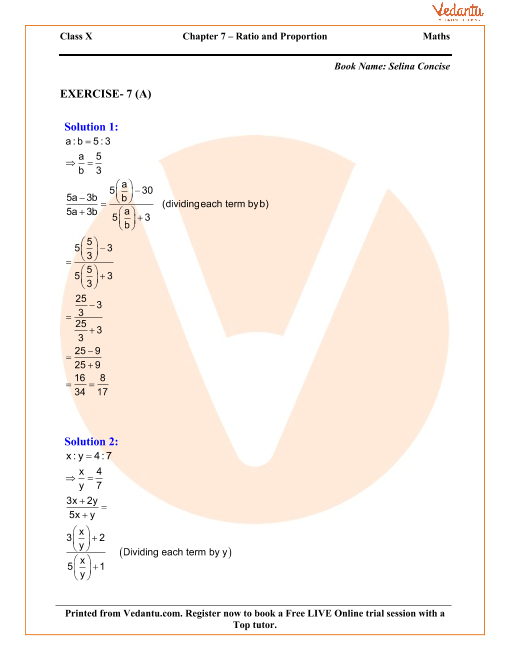
Other Exercises. Question 1. If a: b = 5: 3; find: Solution: Question 2. If x: y = 4: 7; find the value of (3x + 2y): (5x + y). Solution: Question 3. If a: b = 3: 8, find the value of Solution: Question 4. If (a – b): (a + b) = 1: 11, find the ratio (5a + 4b + 15): (5a – 4b + 3).

Solution: (a – b): (a + b) = 1: 11 Let a – b = x, then a + b = 11x Adding we get, 2a = 12x ⇒ a = 6x Subtracting, -2b = -10x ⇒ b = 5x Question 5. Find the number which bears the same ratio to that does to.

Solution: Let x be the required number, then Question 6. Solution: Question 7.

Find; when x² + 6y² = 5xy. Solution: Question 8. If the ratio between 8 and 11 is the same as the ratio of 2x – y to x + 2y, find the value of Solution: Question 9. Divide ₹ 290 into A, B and C such that A is of B and B: C = 4: 3. Solution: Total amount = ₹ 1290 A = B and B: C = 4: 3 ⇒ A: B = 2: 5 and B: C = 4: 3 LCM of 5, 4 = 20 A: B = 2 x 4: 5 x 4 = 8: 20 and B: C = 4 x 5: 3 x 5 = 20: 15 A: B: C = 8: 20: 15 Sum of ratios = 8 + 20 + 15 = 43 Question 10. A school has 630 students. The ratio of the number of boys to the number of girls is 3: 2.

This ratio changes to 7: 5 after the admission of 90 new students. Find the number of newly admitted boys. Solution: Number of students = 630 Ratio in boys and girls = 3: 2 Question 11. What quantity must be subtracted from each term of the ratio 9: 17, to make it equal to 1: 3?

Selina Publishers Concise Mathematics For Class 7 Solutions Pdf

Solution: Let x be subtracted from each term such that = ⇒ 17 – x = 27 – 3x ⇒ -x + 3x = 21 – 17 ⇒ 2x = 10 ⇒ x = 5 Question 12. The monthly pocket money of Ravi and Sanjeev are in the ratio 5: 7. Their expenditures are in the ratio 3: 5. If each save Rs.

80 every month, find their monthly pocket money. 2012 Solution: Let the monthly pocket money of Ravi and Sanjeev be 5x and 7x respectively. Also, let their expenditure be 3y and 5y respectively. So, 5x – 3y = 80 (i) and 7x – 5y = 80 (ii) Multiplying (i) by 7 and (ii) by 5 and subtracting, we get 4y = 160 ⇒ y = 40 From (i), 5x = 80 + 3 x 40 = 200 ⇒ x = 40 So, monthly pocket money of Ravi = Rs. 200 and monthly pocket money of Sanjeev = Rs. 280 Question 13.

The work done by (x – 2) men in (4x + 1) days and the work done by (4x + 1) men in (2x – 3) days are in the ratio of 3: 8. Find the value of x.